The Basics
- A periodic function is one that repeats itself at regular intervals.
- The period is the interval needed to achieve one full cycle of the curve.
- The distance from the axis of the curve to the maximum point on the curve is called the amplitude (NEVER negative).
- The axis of the wave is the horizontal line midway between the maximum and minimum points of the curve.
The Sine Curve
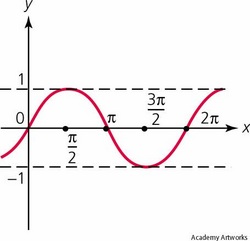
This is the basic sine curve, y = sinx.
The period is 2π and the amplitude is 1.
The range is -1 <= y <= 1.
The period is 2π and the amplitude is 1.
The range is -1 <= y <= 1.
The Cosine Curve
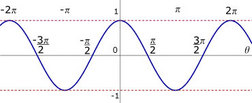
This is the basic cosine curve, y = cosx.
The period is 2π and the amplitude is 1.
The range is -1 <= y <= 1
The period is 2π and the amplitude is 1.
The range is -1 <= y <= 1
Transformations
Transformations of the basic sine curve are represented by this equation:
y = d + a sin (bx-c)
Amplitude = |a| Period = 2π/b Vertical Shift = d Horizontal Shift = c/b
To determine the horizontal and vertical shift of the sine graph begin at the origin (0,0) and go to the first point on the graph where the curve intersects with the axis of the wave.
To determine the horizontal and vertical shift of the cosine graph begin at the (0,a) and go to the first maximum point on the graph.
y = d + a sin (bx-c)
Amplitude = |a| Period = 2π/b Vertical Shift = d Horizontal Shift = c/b
To determine the horizontal and vertical shift of the sine graph begin at the origin (0,0) and go to the first point on the graph where the curve intersects with the axis of the wave.
To determine the horizontal and vertical shift of the cosine graph begin at the (0,a) and go to the first maximum point on the graph.
Tangent Graph
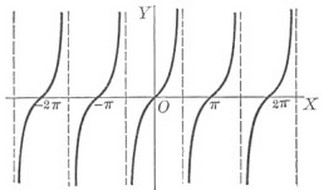
This is the basic tangent curve, y= tanx.
The period is π and there is no amplitude.
Also, on a basic tangent graph, there are asymptotes where the function is not defined. In this case, they are x = π/2 + π or x = π/2 - π.
The range is all real numbers.
The period is π and there is no amplitude.
Also, on a basic tangent graph, there are asymptotes where the function is not defined. In this case, they are x = π/2 + π or x = π/2 - π.
The range is all real numbers.
Cotangent Graph
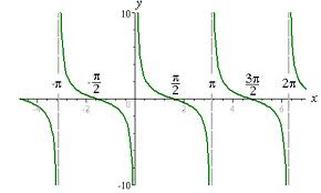
This is the basic cotangent curve, y= cotx.
The period is π and the amplitude is undefined.
The asymptotes occur at x= π+ π or x= π- π
The range is all real numbers.
The period is π and the amplitude is undefined.
The asymptotes occur at x= π+ π or x= π- π
The range is all real numbers.
Cosecant Curve
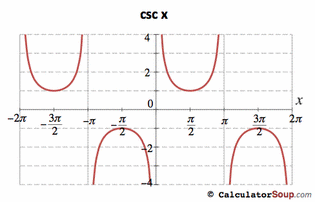
This is the basic cosecant curve, y = cscx.
The period is 2π and the amplitude is undefined.
The asymptotes occur at x = π + π or x = π - π.
The range is y<= -1 or y>= 1
The period is 2π and the amplitude is undefined.
The asymptotes occur at x = π + π or x = π - π.
The range is y<= -1 or y>= 1
Secant Curve
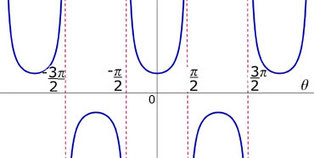
This is the basic secant curve, y = secx.
The period is 2π and the amplitude is undefined.
The asymptotes occur at x = π/2 + π or x = π/2 - π.
The range is y<= -1 or y>= 1
The period is 2π and the amplitude is undefined.
The asymptotes occur at x = π/2 + π or x = π/2 - π.
The range is y<= -1 or y>= 1
Remember!
- Amplitude is NEVER a negative value!
- The b value is NOT the period. Remember this formula: Period = 2π/b
- The period for the basic tangent and cotangent functions is π, not 2π. The range for these two is the set of all real numbers.
- The range for the basic cosecant and secant functions is undefined.
